What do we have to do with change?

I change everyday. You change everyday. The world changes everyday. Therefore, we must study change.
So, here’s a problem: Find the area of a circle.
It’s just πR2, but did you ever think about where it comes from?
π, well that’s just the ratio of the circumference of the circle to it’s diameter, by definition.
Okay, so we know the circle’s perimeter, but how can this be used to find the area?
Remove the “inside” area, leaving yourself with a ring of negligible thickness, say of radius of curvature r. Call the “negligible” thickness dr. Then, what is the area of the ring? It’s, like a rectangle, 2πrdr.
Wait, but it isn’t a rectangle! However, we can make dr as small as possible, therefore forming a rectangle (a weird one)..
Fine, we know a small area, but how do we find the entire area?
r varies from 0 to R, and the small area has to be added up continuously to give the area of the circle.
But how do we add up the area??
Let’s draw a graph of 2πr with r, which is, obviously, linear.
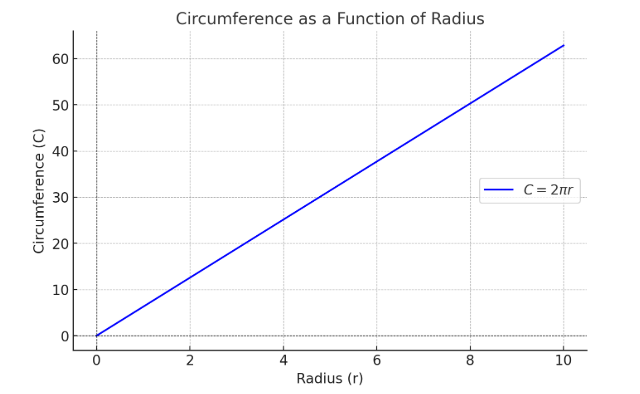
What’s the area? It’s the area under the graph shown.
But wasn’t it a discrete sum? We’ve approximated it.
So, the area is just 0.5*2*pi*r*r= pi*r^2
Intuition behind differentiation and integration:-
You’re given a particle’s position as a function of time. What is it’s speed?
Speed is, by definition, the rate of change of the particle’s position (modulus), and so we need to find the rate of change of positionnn at the instant being considered, which is
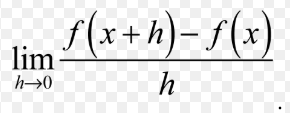
basically the slope of the graph, but calculated for small nudges in x values.
Now, you’re given the derivative of a function, and you need to find the function, we’ve seen that you need to find the area under the graph of the function as a function of the x coordinate, which has been proved to be the reverse of differentiation, namely, integration!
Integration is defined in the following way->
Integration is the continuous analog of a sum. Basically, it’s a sum, but “continuous”. (not 1+2+3+…, it’s 1+(1+dx)+((1+dx)+dx)+…..)
for example, integrating x with respect to dx from 0 to x means finding the area under the graph of 0 to x, which can be easily evaluated as 0.5x^2, but for other functions, we need to see that the derivative of the integral (indefinite) returns the function itself (fundamental theorem of calculus), and therefore, we see that the derivative of 0.5x^2 is just x, verifying the definition.


