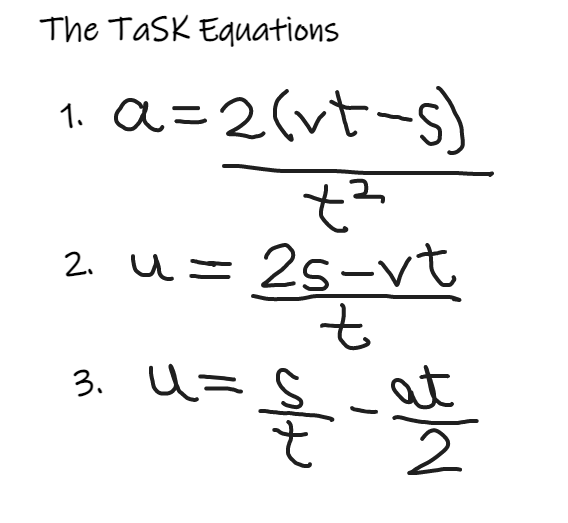FIRST, WHAT IS MOTION?

Motion is perceived when something’s position changes with respect to time and it’s surroundings.
It is measured usually in the form of distance and displacement
WHAT IS DISTANCE AND DISPLACEMENT?

Distance is defined as the actual length of the path traversed by the body, in short how much the body moves. It’s SI unit is m and other units include mm, km, cm, mi etc. It is a scalar quantity, which means it only has magnitude but no direction.
Displacement is defined as the shortest path length between a body’s final and initial position. It is a vector quantity thus while specifying displacement, we need to take into consideration direction of motion too. Along a coordinate plane where the final and initial position of an object are marked, we have 2 coordinates on the plane (sometimes 3, but that is in case of 3 dimensional motion, which will not be considered because we are discussing motion along a straight line here), which are x-coordinate and y-coordinate. Here if a body moves from an initial point (a,b) to (c,d) then the displacement of the body (shortest path length) will be √[(c-a)²+(d-b)²], which is the distance formula. [square is an operation which means; a²=a*a]
WHAT ARE THE VARIOUS TERMS USED IN MOTION?

Apart from distance and displacement, there are also many other terms used when describing motion. Those are speed, velocity and acceleration (which will be further used in the Primary Equations of motion to derive the TaSK equations).
Speed (you hear it often) is defined as the rate at which something moves.
Speed = distance/time = s/t
Velocity is defined as the speed in a particular direction.
Velocity = displacement/time = V = S/t [Bold print represents vectors]
Acceleration is defined as the rate of change of velocity
a = [v–u]/t where a= acceleration; v= final velocity; u=initial velocity and t= time
NOW, WHAT ARE THE PRIMARY EQUATIONS OF MOTION?

The following are the equations of motion:-
v = u + at
s = ut + 1/2*at²
v²-u²=2as
Using this, the 3 TaSK Equations will be derived.
THE TaSK EQUATIONS
The 1st TaSK Equation:-
From the equations of motion, if we try to take out the value of u or the initial velocity, we get;
1st eq.- v=u+at => u = v-at………(1)
2nd eq.- s=ut+1/2at² => ut = s-1/2at² => u = s/t – at/2………..(2)
3rd eq.- v²-u²=2as=> -u²=2as-v² => u² = v²-2as => u=√(v²-2as)……………..(3)
Now, comparing equations 1 and 3, we get,
v-at= √(v²-2as)
Square both sides,
v² + a²t² – 2vat = v² – 2as [ (a-b)²=a²+b²-2ab ]
Simplifying and taking ‘a’ common ,
a²t² – 2vat = -2as
a(at²-2vt) = a(-2s)
Canceling out ‘a’,
at²-2vt=-2s
Simplifying,
2vt-at²=2s
-at² = 2s-2vt
at² = 2vt-2s
a = [2vt-2s]/t²
a = 2(vt-s)/t²…………..(4) – The 1st TaSK Equation ………….. which is independent of the initial velocity of the body even though it may not be 0
Thus, the first TaSK equation is a = 2(vt-s)/t²
Now, for the second TaSK equation, inputting equation (4) into equation (2),
u = s/t – {[(2vt-2s)/t²][t]}/2
u = s/t – (vt-s)/t
u = [s-(vt-s)]/t
u = [2s-vt]/t……………….(5) – The 2nd TaSK Equation ………….which is independent of acceleration even though there is acceleration
Thus, the first TaSK equation is u = [2s-vt]/t
Now, for the third TaSK equation, which is an alternate way of proving that the average velocity is equal to the quotient obtained when the total distance is divided by total time too,
From result (5),
u = [2s-vt]/t
u = 2s/t – vt/t
u = 2s/t – v
Transposing v,
u+v = 2s/t
=> v = 2s/t-u…………….(6)
From equation (1),
u = v-at
=:> v = u + at……………(7)
Comparing equations (6) and (7)
2s/t – u = u +at
=> 2u = 2s/t – at
=> u = s/t – at/2 …….(8) The Third TaSK Equation which is independent of the final velocity of the body even though it is present
Thus, the third TaSK equation is u = s/t – at/2
ENDNOTE
The 3 TaSK equations are:-